 Carl Friedrich Gauss
Carl Friedrich GaussA truly incomparable mathematician who had a major influence in various areas of maths even at a very young age. I cannot name even a fraction of his various contributions to mathematics but they include:
- The construction of a heptadecagon (17 sided shape) with just a straight edge and compass, as shown in Numberphile's recent video.
- The Prime Number Conjecture
- The fundamental theorem of algebra
- Advances in Modular Arithmetic (a post on this should soon follow)
- and over 100 different theorems, ideas, methods and lemmas named after him
Suffice it to say, he has had an incredible influence in almost all areas of maths since the 18th century.
Euclid
 Euclid, the classic Greek mathematician, was a person who revolutionised maths, introducing and developing whole fields of mathematics, especially geometry (he is known as the 'Father of Geometry') and axiomatic theory.
Euclid, the classic Greek mathematician, was a person who revolutionised maths, introducing and developing whole fields of mathematics, especially geometry (he is known as the 'Father of Geometry') and axiomatic theory.His most prominent work, the Elements, set the way for maths in the following millenia and until the 21st century was the second most sold work worldwide, following only the Bible.
One of his most important ideas he put into practice was the use of axioms, specifically the 5 Postulates from which all his proofs came:
1. A straight line segment can be drawn joining any two points.
2. Any straight line segment can be extended indefinitely in a straight line.
3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
4. All right angles are congruent.
5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the parallel postulate.
You'll note that the 5th is rather more complex than the other four, but that is also a story for another post...
Leonhard Euler
 I don't know whether I can put this better than Laplace when he said:
I don't know whether I can put this better than Laplace when he said:"Read Euler, read Euler, he is the master of us all."
Euler made great discoveries, like all in this list, in various areas of maths but there is one which I associate most strongly with Euler: Euler's Identity.
Euler's identity is what some, if not most, mathematicians call the greatest work of maths as it links seemingly distinct areas of maths in a wonderfully simple and concise equation:
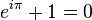
where:
- 'e' is the base of the natural logarithm, fundamental in calculus and discovered by Gauss to be linked strongly with the primes
- 'π' is the ratio between the circumference and diameter of a circle, fundamental to Euclidean and non-Euclidean geometry (named after Euclid of course)
- 1 is the multiplicitive identity, i.e. anything multiplied by 1 is itself
- 0 is the additive identity, i.e. anything add 0 is itself
This simple equation links all of these together and is in my opinion the greatest result in mathematics ever.
Pierre de Fermat
 Unlike the others in this list, Fermat was an amateur mathematician but, as E.T. Bell put it, the 'Prince of Amateurs'.
Unlike the others in this list, Fermat was an amateur mathematician but, as E.T. Bell put it, the 'Prince of Amateurs'.He was most famous probably for not what he did, but what he didn't do. He was famed for claiming he had solved big problems without releasing his proofs, most famously in the case of 'Fermat's Last Theorem':
"It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvellous proof of this, which this margin is too narrow to contain."
The jury is still out as to whether he actually solved it or not, but given that it was only solved 358 years later using areas of mathematics as yet undiscovered, it seems unlikely.
However that does not detract from his brilliance as a mathematician.
Srinivasa Ramanujan

Ramanujan, the most modern mathematician in this list, was an exceptional person. Untrained, self-taught and a bit mad (who isn't?), he was brought over to England by G. H. Hardy, author of A Mathematician's Apology, after the exchange of a number of letters which revealed Ramanujan to be a truly incredible mathematician.
In his comparatively short mathematical life, he came up with around 3900 results notably making progress towards areas of maths including infinite series, continued fractions,...
As Erdős recollected, "Suppose that we rate mathematicians on the basis of pure talent on a scale from 0 to 100, Hardy gave himself a score of 25, J.E. Littlewood 30, David Hilbert 80 and Ramanujan 100."
But what he is now most famous for outside of mathematical circles is the taxicab story, which highlights the brilliance of this man:
"I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. "No", he replied, "it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways."
A few others:
- Blaise Pascal
- Pythagoras
- Archimedes
- Isaac Newton
- Gottfried Wilhelm Leibniz
- René Descartes
- David Hilbert
- Évariste Galois
- Kurt Gödel
- Andrew Wiles






